Scripting Ropes

Most Obi actors have static topologies: the amount of particles and the way constraints connect them doesn't change over time. This is the case for regular cloth, skinned cloth, rods, bones and softbodies. However there's some exceptions, and ropes are one of them. Ropes can be torn, and their length can change at runtime (by using cursors). These events change the amount of active particles and constraints in the rope, as well as their order in the actor's arrays.

Elements

When dealing with ropes you can't assume particles will appear in the rope.solverIndices array in the same order they do in the rope. For instance, the following code to get the first and last particles in the rope is wrong:

// this is wrong!
int firstParticle = rope.solverIndices[0];
int lastParticle = rope.solverIndices[rope.solverIndices.count-1];

The above code won't work - meaning it may return the index of particles that are anywhere along the rope - for a couple reasons:

• Not all particles in the rope are active at first. Ropes preallocate a pool of extra particles which start out deactivated. The particles in this pool will be activated at runtime when new particles are required by the rope (because it has been torn or its length has increased) or deactivated when no longer needed (because rope length has decreased). You can control the amount of extra pooled particles in the rope blueprint.


• As particles are activated/deactivated, they are not always appended at the end of the rope: they might be added/removed from any position in the rope!

So if particles can become active/inactive and arbitrarily reordered at runtime, how can we access data at a specific point in the rope in a consistent manner? the answer is by using elements.

ObiStructuralElement is a small data structure that references 2 particles. Every rope contains an elements list. All elements in this list are guaranteed to stay ordered relative to their position along the rope, and the amount of elements is guaranteed to be equal to the amount of active particles minus one (or the amount of active particles, for a closed rope). You can think of them as the "edges" in between particles:

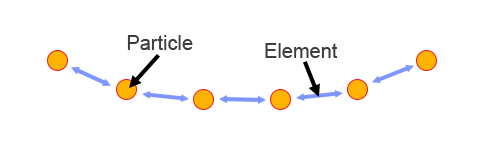
Each element in the array contains the indices of two particles in the solver: particle1 and particle2.

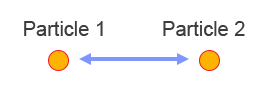
Using elements, we can robustly get the first and last particles in the rope (or any in between!), even if particles are activated/deactivated/reordered at runtime:

// first particle in the rope is the first particle of the first element:
int firstParticle = rope.elements[0].particle1;

// last particle in the rope is the second particle of the last element:
int lastParticle = rope.elements[rope.elements.Count-1].particle2;

// now get their positions (expressed in solver space):
var firstPos = rope.solver.positions[firstParticle];
var lastPos  = rope.solver.positions[lastParticle];

Tearing ropes at runtime

Elements play an important role in rope tearing/cutting. You can tear a rope at any given point by calling rope.Tear() and passing the element you want to tear. This will introduce a discontinuity between that element and the previous one in the rope, by activating one extra particle from the pool and re-connecting the element to it:

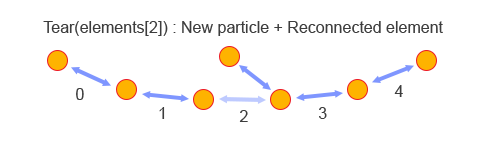
After you change the rope's topology by tearing it, you must call rope.RebuildConstraintsFromElements();. This will regenerate all internal rope constraints to follow the new topology described by the elements. It's a relatively slow operation, so if you're going to tear the rope multiple times in a single frame, it's a good idea to call RebuildConstraintsFromElements() just once at the end to amortize its cost.

Here's a more complex example that combines element usage and tearing to cut all rope elements that intersect a line segment in screen-space. This can be used to allow players to cut ropes by sweeping across the screen with the mouse cursor. You can find this code being used in the included Obi/Samples/RopeAndRod/RopeCutting sample scene.

/**
* Cuts the rope using a line segment, expressed in screen-space.
*/
private void ScreenSpaceCut(Vector2 lineStart, Vector2 lineEnd)
{
	// keep track of whether the rope was cut or not.
	bool cut = false;

	// iterate over all elements and test them for intersection with the line:
	for (int i = 0; i < rope.elements.Count; ++i)
	{
		// project the both ends of the element to screen space.
		Vector3 screenPos1 = cam.WorldToScreenPoint(rope.solver.positions[rope.elements[i].particle1]);
		Vector3 screenPos2 = cam.WorldToScreenPoint(rope.solver.positions[rope.elements[i].particle2]);

		// test if there's an intersection:
		if (SegmentSegmentIntersection(screenPos1, screenPos2, lineStart, lineEnd, out float r, out float s))
		{
			cut = true;
			rope.Tear(rope.elements[i]);
		}
	}

	// If the rope was cut at any point, rebuild constraints:
	if (cut) rope.RebuildConstraintsFromElements();
}

/**
* line segment 1 is AB = A+r(B-A)
* line segment 2 is CD = C+s(D-C)
* if they intesect, then A+r(B-A) = C+s(D-C), solving for r and s gives the formula below.
* If both r and s are in the 0,1 range, it meant the segments intersect.
*/
private bool SegmentSegmentIntersection(Vector2 A, Vector2 B, Vector2 C, Vector2 D, out float r, out float s)
{
	float denom = (B.x - A.x) * (D.y - C.y) - (B.y - A.y) * (D.x - C.x);
	float rNum = (A.y - C.y) * (D.x - C.x) - (A.x - C.x) * (D.y - C.y);
	float sNum = (A.y - C.y) * (B.x - A.x) - (A.x - C.x) * (B.y - A.y);

	if (Mathf.Approximately(rNum, 0) || Mathf.Approximately(denom, 0))
	{  r = -1; s = -1; return false; }

	r = rNum / denom;
	s = sNum / denom;

	return (r >= 0 && r <=1  && s >= 0 && s <= 1);
}