(19-05-2022, 03:11 PM)locque Wrote: It's basically how a real scale would work, the plate of the scale is locked on the y axis and propped up by spring joint. The script takes the local y position of the plate when turning it on as a baseline and then tracks the the height differential to that point.
This assumes an infinitely small timestep, which is true in the real world (since time is continuous) but not at all in a simulation, where time is discrete. Every simulation step, position is integrated from velocity, and velocity from acceleration.The accuracy of the integration is affected by the timestep length, being better the smaller the timestep is.
The following graph shows the trajectory of an object integrated using Euler's method (a variant of which is the most widely used one in realtime physics engines): As you can see, the simulated trajectory significantly diverges from the real one over time:
![[Image: Graphical-representation-of-Euler-integr...method.jpg]](https://x-engineer.org/wp-content/uploads/2018/10/Graphical-representation-of-Euler-integration-method.jpg)
If you were to measure the mass of the object using its position at time T (assuming a given impulse at T=0), you'd underestimate it. By chopping up time into smaller chunks, you'd get a piecewise linear approximation that's closer to the real thing.
By using positional deltas to measure weight instead of forces/impulses you're measuring the approximation of an approximation, the quality of which depends on the timestep length used. To make things worse constraint corrections aren't instantly propagated, so the more objects you add on top of your scale, the less precise it will be.
The usual way to implement a scale in a game is to measure contact impulses between the scale plate and the object(s) being weighted, convert these to forces (dividing by the timestep) and then divide by gravitational acceleration to get mass. Imho you should try this, this is what I assumed you were doing in the first place and why I asked if you were using the full timestep length or the substep length to perform this calculation.
(19-05-2022, 03:11 PM)locque Wrote: That doesn't seem to be the way it works, decreasing the fixed timestep has almost no effect on the fluid behaviour compared to raising the solver substeps.
This is the expected behavior:
A) Using a timestep of X and 8 substeps yields an effective timestep length of X/8.
B) Using a timestep of X/8 seconds and 1 substep yields an effective timestep length of X/8/1 = X/8.
As you see, the timestep used by the fluid simulation is the exact same in both cases, so the behavior of the fluid should be pretty much identical in A) and B). Any differences are due to collision detection being performed only once per full step, and reusing the results over all substeps.
However, in case A)
the timestep used by Unity's physics engine is X but the one
used by Obi is eight times smaller. In case B,
both engines use a timestep of X/8,
which increases the accuracy of Unity's physics simulation as well.
The reason why I suggested to try B) is to improve your weighting scale precision by using a smaller timestep for Unity's simulation, while keeping identical fluid behavior.


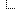



![[Image: Graphical-representation-of-Euler-integr...method.jpg]](https://x-engineer.org/wp-content/uploads/2018/10/Graphical-representation-of-Euler-integration-method.jpg)